Impressum Kontakt Disclaimer
Mathematik Textaufgaben Klasse 7
Leichte Übungsaufgaben sind mit 
und
anspruchsvolle Aufgaben mit 
gekennzeichnet.
Autor: admin - Vorschläge willkommen!
Beim Lösen von Textaufgaben empfiehlt es sich, 2 bis 3 mal zu lesen, bevor man anfängt zu überlegen. So versteht man Zusammenhänge und findet den Lösungsweg.
Alle Aufgaben entsprechen dem Niveau von typischen Prüfungsaufgaben - sorgfältig zusammengestellt.
| Die Lösung leuchtet auf, wenn der Mauszeiger auf das ? zeigt |  |
|---|---|
| 1) Dreisatz: Welches Angebot ist besser? 20 Flaschen Limo zu 0,5 l für 10,99 EUR oder 24 Flaschen Limo zu 0,33 l für 9,99 EUR? Runde auf ganze Cent. | |
| 2) Dreisatz: 11 Erntehelfer benötigen für einen Erdbeeracker 15 Stunden. Mit wieviel Stunden müssen 4 Erntehelfer rechnen? | |
| 3) Prozentrechnung: Vor Weihnachten 2009 wurde ein Computer um 14% teurer und kostete dann 639 EUR. Im Januar 2010 wurde der Preis 23% gesenkt. Ermittle den Ursprungspreis sowie den letzen Preis. | |
| 4) Proportional oder antiproportional...? Über eine Zuordungstabelle kann man es feststellen. Was bedeutet Quotiengleichheit und Produkgleichheit? | |
| 5) a) Zinsrechnung: Günter legt 4500 EUR zu 4,8% an. Wieviel EUR hat er nach 4 Jahren ohne jährliche Zinsauszahlung? Runde pro Jahr auf ganze Cent. b) Jürgen darf sein Konto bis 3000 EUR überziehen. Genau 3 Monate steht er mit dieser Summe im Minus. Sein Großvater sorgt danach mit einer großzügigen Zahlung für einen Kontostand im Plus. Berechne die Summe, die in den 3 Monaten über einen Überziehungskredit zum Zinssatz von 13,5% angefallen ist. angefallen ist. c) Marie legt Geld an auf einem Geldmarktkonto. Sie erhält Zinsen in Höhe von 3,6 % pro Jahr. Nach 7 Monaten hebt sie ihr Erspartes samt Zinsen komplett ab. Die Zinsen betragen 105,00 EUR. Wieviel hatte sie ursprünglich angelegt? | |
| 6) Zinseszins: Ein Kunde legt 5000 EUR auf 5 Jahre fest an zum Jahreszinssatz von 3,9%. Auf welche Summe ist seine Anlage am Ende angewachsen? | |
| 7) Geometrie: Wie berechnet man die Winkelsumme eines Vielecks? | |
| 8) Mit welcher Formel läßt sich die Anzahl der Diagonalen eines Vielecks berechnen? | |
639 EUR x 0,77 (oder mit mehr Aufwand 639 EUR - (639 EUR x 23/100) = 492,03 EUR (letzter Preis). Ergibt der Quotiont der zugeordneten Größe y und der zugeordneten Größe x für jede Reihe aus der Tabelle dasselbe Ergebnis, dann gibt der Proportionalitätsfaktor q Proportionalität vor (Zugeordnete Größe y : zugeordnete Größe x = q).
Bei Antiproportionalität hilft die Formel für Produkgleichheit. Es ergibt sich die Gesamtgröße g über die Formel Ausgangsgröße x multipliziert mit Ausgangsgröße y.
Auch hier ist die Gesamtgröße g pro Tabellenreihe stets gleich. a) Nach 4 Jahren: 5428 EUR
b) 101,25 EUR
c) Lösung: 5000,- EUR - Rechenweg:
105,00 EUR : 7 x 12 : 3,6 x 100 = 5000 EUR 6) Formel: Endkapital = Startkapital x (1 + Prozentsatz)^Jahre
...also 5000 x (1,039)^5 = 5000 x 1,210814847 = 6054,07 EUR nach 5 Jahren 7)
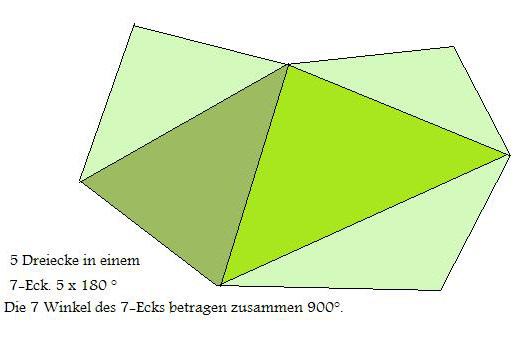Man legt Verbindungslinien im Inneren des Vielecks an, die sich gegenseitig nicht überschneiden dürfen.
Es entstehen Dreiecke oder ein Viereck, wenn man dieses nicht auch in 2 Dreiecke unterteilt. Man zählt die Dreiecke im Vieleck
ab und multipliziert sie mit 180 Grad - der Winkelsumme eines Dreiecks. Ein Viereck hat 360 Grad.
Formel für die Winkelsumme eines Vielecks: W = (Eckenanzahl n - 2) x 180°
7) Anzahl der Diagonalen eines n-Ecks = [n x ( n - 3)] : 2
Script geschützt durch: GNU Lesser General Public License (LGPL)