Lerninfos für Jung und Alt
Lerninfos für Jung und Alt
Impressum Kontakt Disclaimer Für eine optimale Darstellung auf dem Smartphone bitte das Querformat verwenden.
Die Erläuterungen in den Darstellungen sind leider nur in deutscher Sprache lesbar.
Grundrechenarten Mathematik
Schriftliches Subtrahieren mit Subtrahend und Minuend - Rechnen von Hand:
Schriftliche Addition
Das Schaubild erläutert die schriftliche Addition. Summe nennt man das Ergebnis aus der Addition vonmindestens 2 Summanden.
Schriftliche Division und Multiplikation.
Das Schaubild zeigt anhand von Beispielen, wie schriftlich dividiert wird (mit Divident, Divisor und Quotient),ebenso die schriftliche Multiplikation (mit Faktor und Produkt). Im Zeitalter des Taschenrechners geraten
auch diese handschriftlichen Rechnungen schnell in Vergessenheit:
Die häufigsten Fehlerquellen liegen im Nichterkennen einer Null im Ergebnis. Die Probe sorgt für Sicherheit.
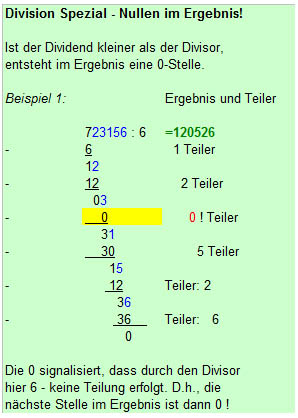
schriftliches Rechnen mit Dezimalbrüchen (KLASSE 6)
Beim schriftlichen Addieren von Dezimalbrüchen werden Summanden so untereinander geschrieben, dass Komma unter Komma erscheint. Beispiel:
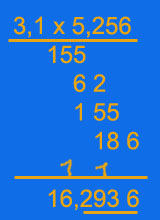
Beim Subtrahieren von Dezimalbrüchen wird genauso verfahren.Im Ergebnis erscheint das Komma dann an der entsprechenden Stelle. Bei der Multiplikation von Dezimalbrüchen wird das Komma zunächst
ignoriert. Im Ergebnis wird die Summe der Nachkommastellen beider Faktoren
von rechts nach links abgestrichen. Beispiel:
Für vereinfachtes Rechnen z.B. im Kopf kann man eine Kommaverschiebungsregel nutzen,die beim schriftlichen Ausrechnen eigentlich nichts bringt. In einem der beiden Faktoren kann man
den Dezimalbruch in eine natürliche Zahl verwandeln. Dabei verschiebt man das Komma
um bestimmte Stellen nach rechts. Im Gegenzug muss im anderen Faktor das Komma um
die gleiche Anzahl in die Gegenrichtung verschoben werden,
um nicht die Werte zu verändern. Beispiele:
Eine weitere Kommaverschiebungsregel gilt bei derschriftlichen Division von Dezimalbrüchen. Hier muss der Divisor
in eine natürliche Zahl verwandelt werden. Im Gegenzug allerdings wird
das Komma des Dividenden um die gleiche Anzahl der Stellen in dieselbe
Richtung verschoben. Ansonsten verändert man die Werte. Beispiel:
nach oben