Bedeutung des Maßstabs auf Karten - Übung

von admin

Auf Landkarten weist der Maßstab auf eine Verkleinerung oder eine Vergrößerung hin.

Beispiel für eine Verkleinerung: Maßstab 1:10000 bedeutet, dass 1cm auf der Karte in Wirklichkeit 10000cm in der Natur sind, z.B. die 100m-Bahn auf einem Sportplatz ist auf der Karte nur 1 cm lang.

Beispiel für eine Vergrößerung: Maßstab 4:1 bedeutet, dass man z.B. ein 1 Bild 4fach vergrößert. Aus 1cm Seitenlänge werden 4cm Seitenlänge.

Man muss dann nur noch wissen, dass man bei der Umrechnung in Meter 2 Nullen abstreichen muß. 1km sind 1000m. Damit kann man Strecken zwischen 2 Punkten auf einer Karte (Luftlinie oder Straßenverläufe) berechnen. Im Folgenden gibt es eine kleine Übung zum Ausdrucken:

- einfach auf das Druck-Element unten klicken Akrobat Reader notwendig

Aufgabe: Berechne die wirkliche Entfernung in km zwischen den Strecken-Fähnchen...

beim Abmessen mit dem Lineal versuchen millimetergenau die an der Verbindungslinie zu arbeiten (Druckdiffernzen möglich).

1) von A-Dorf zum Waldsee/B-Dorf/Kirche/Fluß
2) von B-Dorf zum Waldsee/Kirche/Fluß
3) vom Waldsee zum Fluß/Kirche
4) vom Fluß zur Kirche

1) A-Dorf-Waldsee: 10,3 cm x 50000 in der Natur = 515000 cm = 5150 m = 5,15 km

---

A-Dorf zu B-Dorf: 11 cm x 50000 = 550000cm = 5500 m = 5,5 km

---

von A-Dorf zur Kirche: 23,2 cm x 50000 = 1160000 cm = 11600 m = 11,6 km

---

von A-Dorf zum Fluß: 18,5 cm x 50000 = 925000 cm = 9250 m = 9,25 km

2) von B-Dorf zum Waldsee: 10,4 cm x 50000 cm = 520000 cm = 5200 m = 5 km

---

von B-Dorf zur Kirche: 11,7 cm x 50000 cm = 585000 cm = 5850 m = 5,85 km

---

von B-Dorf zum Fluß: 13 cm x 50000 cm = 650000 cm = 6500 m = 6,5 km

---

1) vom Waldsee zum Fluß: 23,2 cm x 50000 cm = 1160000 cm = 11600 m = 11,6 km

---

vom Waldsee zur Kirche: 20,9 cm x 50000 cm = 1045000 cm = 10450 m = 10,45 km

---

1) vom Fluß zur Kirche: 13,6 cm x 50000 cm = 680000 cm = 6800 m = 6,8 km

---

***PDF - ÜBUNGSBLATT ZUM AUDRUCKEN***

---

Thema:

Gewichte und Hohlmaße

von admin

Bei der Umrechnung von Gewichten sind folgende Maßeinheiten zu berücksichtigen:
Gramm (g), Milligramm (mg), Kilogramm (kg) sowie Tonne (t).

Es gilt: 1 g = 1000 mg
1000 g = 1 kg
1000 kg = 1 t

Die folgende Übung hilft bei den gängigen Umrechnungen von Gewichten.
Hinter dem Fragezeichen verbirgt sich die Lösung.

Übung mit Gewichten:

Umrechnungen	50 kg	12 g	1 t	1/2 kg	355 g	9 kg	3/4 t	801 kg	1/4 t
Gramm (g)
Kilogramm (kg)
Tonnen (t)

50.000 g 12 g 1000.000 g 500 g 355 g 9000 g 750.000 g 801.000 g 250.000 g 50 kg 0,012 kg 1000 kg 0,5 kg / 0,500 kg 0,355 kg 9 kg 750 kg 801 kg 250 kg 0,05 t / 0,050 t 0,000012 t 1 t 0,0005 t 0,000355 t 0,009 t 0,750 t 0,801 t 0,25 t / 0,250 t

Der Liter als Hohlmaß

Auch beim Umrechnen von Hohlmaßen kommt den Stellen vor oder nach dem Komma besondere Bedeutung zu.

Ein typisches Hohlmaß ist der definierte Liter (l).
Es gilt: 1 l = 1000 ml (Milliliter)
D.h., dass 350ml dann 0,350 l sind oder 1,5 l = 1500 ml oder 1ml entsprechen 0,001 l.

Folgende Tabelle veranschaulicht die Anzahl der einzelnen Stellen bei entsprechender Literzahl:

	100 l	10 l	1 l	100 ml	10 ml	1 ml
14 l	0	1	4	0	0	0
8,3 l	0	0	8	3	0	0
425 ml	0	0	0	4	2	5
6558,5 l	65	5	8	5	0	0

Thema:

Maße - Quiz mit Längen / Flächen - mehrere Antworten möglich!

von admin

Voraussetzungen zum Lösen der Übung sind Umwandlungsfaktoren:
1 mm x 10 = 1 cm
1 cm x 10 = 1 dm
(die Bezeichnung dm kommt aus dem Lateinischen: decimus: der 10te (hier Zentimeter!)
1 dm x 10 = 1 m
1 m x 1000 = 1 km

Daraus ergeben sich: 1000000 mm sind 1km = 100000 cm =10000 dm = 1000 m = 1 km

Man kann sich einfach merken, dass immer der Faktor 10 beim Umwandeln dazwischen liegt.
Zu beachten ist, dass von cm auf m (häufig gebraucht) mit dem Faktor 100 multipliziert werden muss. Man ermittelt die Anzahl der Nullen, die nach links oder rechts der Zahl wandern.

Beispiel: 350 cm sind wieviel km? Faktoren ermitteln gemäß Reihenfolge: cm-dm-m-km (5 Nullen!): Das Komma wandert bei der Zahl 350 nun 5 x von rechts nach links: ,00350 - also 0,0035 km. Beispiel 2: 681 m in cm umwandeln:

Anzahl der Faktoren ermitteln: m-dm-cm, also 10x10=100; diese x 681. Ergebnis: 68100 cm sind 681m .

Bei der Berechnung von rechteckigen Flächen muss die Maßeinheit identisch sein: Beispiel: 400 cm x 3 m = 4 m x 3 m = 12m² oder 400 cm x 300 cm = 1200 cm²

---

Wie rechnet man Strecken, Flächeninhalts- und Raummaße möglichst effektiv um?

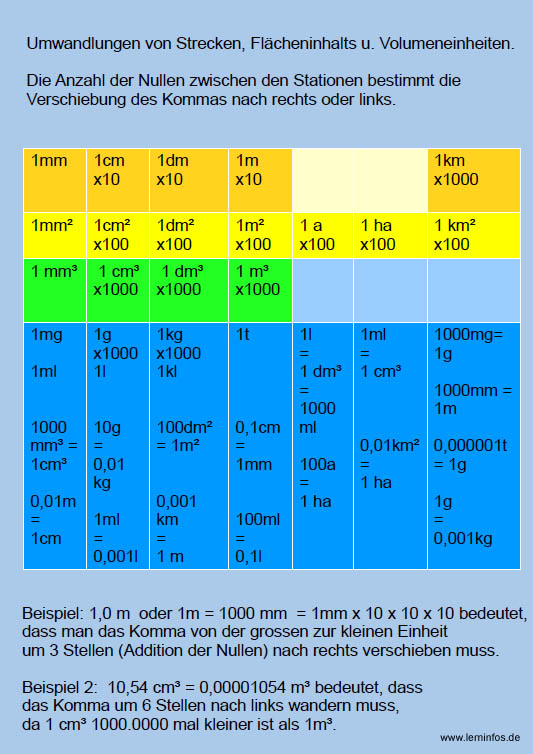
Hierbei geht es um Kommaverschiebungen nach links (Umrechnung vom kleinen zum größeren Maß
oder Kommaverschiebung nach rechts (Umrechnung vom großen zum kleineren Maß. Bei natürlichen Zahlen muss man sich z.B. statt einer "4" eine "4,0" denken. Nullen entstehen zusätzlich immer dann, wenn an entsprechender Stellenwertposition Zahlen von 1 bis 9 nicht auftreten.

Und nun zum Schaubild, in dem zu beachten ist, dass "10, 100 oder 1000" unter den Einheiten
auf das Ergebnis des Vielfachen der kleineren Einheit hinweist.

Impressum Kontakt Disclaimer

nach oben

STARTSEITE
© 2009 - dato